# Check if installed and load
# Simple Features, used for working with spatial data.
library(sf) # Simple Features, spatial data manipulation
library(dplyr) # Data manipulation and transformation
library(ggplot2) # Data visualization
library(tmap) # Thematic maps
library(mapview) # Interactive maps
library(basemapR) # Static maps
library(ggspatial) # Spatial visualization with ggplot2
library(viridis) # Color palettes for data visualization
library(raster) # Raster data manipulation
library(colorspace) # Color manipulation and palettes
# Spatial and Spatio-Temporal Geostatistical Modelling, Prediction, and Simulation
library(gstat) # Geostatistical modeling
library(spatstat) # Spatial point pattern analysis
# Clustering and Dimensionality Reduction
library(dbscan) # Density-based spatial clustering
library(fpc) # Flexible procedures for clustering
library(eks) # Kernel density estimation and clusteringLab
Points
Points are spatial entities that can be understood in two fundamentally different ways. On the one hand, points can be seen as fixed objects in space, which is to say their location is taken as given (exogenous). In this case, analysis of points is very similar to that of other types of spatial data such as polygons and lines. On the other hand, points can be seen as the occurence of an event that could theoretically take place anywhere but only manifests in certain locations. This is the approach we will adopt in the rest of the notebook.
When points are seen as events that could take place in several locations but only happen in a few of them, a collection of such events is called a point pattern. In this case, the location of points is one of the key aspects of interest for analysis. A good example of a point pattern is crime events in a city: they could technically happen in many locations but we usually find crimes are committed only in a handful of them. Point patterns can be marked, if more attributes are provided with the location, or unmarked, if only the coordinates of where the event occured are provided. Continuing the crime example, an unmarked pattern would result if only the location where crimes were committed was used for analysis, while we would be speaking of a marked point pattern if other attributes, such as the type of crime, the extent of the damage, etc. was provided with the location.
Point pattern analysis is thus concerned with the description, statistical characerization, and modeling of point patterns, focusing specially on the generating process that gives rise and explains the observed data. What’s the nature of the distribution of points? Is there any structure we can statistically discern in the way locations are arranged over space? Why do events occur in those places and not in others? These are all questions that point pattern analysis is concerned with.
This notebook aims to be a gentle introduction to working with point patterns in R. As such, it covers how to read, process and transform point data, as well as several common ways to visualize point patterns.
Installing Packages
Data
We are going to continue with Airbnb data in a different part of the world.
Airbnb Buenos Aires
Let’s read in the point dataset:
# read the AirBnb listing
listings <- read.csv("data/BuenosAires/listings_nooutliers.csv")
summary(listings) id name host_id host_name
Min. : 6283 Length:18572 Min. : 2616 Length:18572
1st Qu.:18460148 Class :character 1st Qu.: 13834944 Class :character
Median :31758329 Mode :character Median : 66033824 Mode :character
Mean :28673848 Mean :108620951
3rd Qu.:40007128 3rd Qu.:188964374
Max. :51100644 Max. :412506828
neighbourhood_group neighbourhood latitude longitude
Mode:logical Length:18572 Min. :-34.69 Min. :-58.53
NA's:18572 Class :character 1st Qu.:-34.60 1st Qu.:-58.43
Mode :character Median :-34.59 Median :-58.41
Mean :-34.59 Mean :-58.42
3rd Qu.:-34.58 3rd Qu.:-58.39
Max. :-34.53 Max. :-58.36
room_type price minimum_nights number_of_reviews
Length:18572 Min. : 218 Min. : 1.000 Min. : 0.00
Class :character 1st Qu.: 1800 1st Qu.: 2.000 1st Qu.: 0.00
Mode :character Median : 2790 Median : 3.000 Median : 3.00
Mean : 5424 Mean : 6.996 Mean : 15.92
3rd Qu.: 4470 3rd Qu.: 5.000 3rd Qu.: 16.00
Max. :962109 Max. :730.000 Max. :500.00
last_review
Length:18572
Class :character
Mode :character
Let’s finish preparing it:
# locate the longitude and latitude
names(listings) [1] "id" "name" "host_id"
[4] "host_name" "neighbourhood_group" "neighbourhood"
[7] "latitude" "longitude" "room_type"
[10] "price" "minimum_nights" "number_of_reviews"
[13] "last_review" listings <- listings %>%
st_as_sf(coords = c(8, 7)) %>% # create pts from coordinates
st_set_crs(4326) # set the crsAdminstrative Areas
We will later use administrative areas for aggregation. Let’s load them.
BA <- read_sf("data/BuenosAires/neighbourhoods_BA.shp") #read shp
BA <- st_make_valid(BA) # make geometry validSpatial Join
# spatial overlay between points and polygons
listings_BA <- st_join(BA, listings)
# read the first lines of the attribute table
head(listings_BA)Simple feature collection with 6 features and 13 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -58.46683 ymin: -34.59783 xmax: -58.43854 ymax: -34.57829
Geodetic CRS: WGS 84
# A tibble: 6 × 14
neighbourh neighbou_1 geometry id name host_id host_name
<chr> <chr> <POLYGON [°]> <int> <chr> <int> <chr>
1 Chacarita <NA> ((-58.45261 -34.59584, -… 24763 Amaz… 1.01e5 Sebastian
2 Chacarita <NA> ((-58.45261 -34.59584, -… 234002 LOVE… 1.23e6 Mariana
3 Chacarita <NA> ((-58.45261 -34.59584, -… 447786 METR… 9.75e5 Alejandro
4 Chacarita <NA> ((-58.45261 -34.59584, -… 589147 Grea… 2.91e6 Marcos
5 Chacarita <NA> ((-58.45261 -34.59584, -… 644840 Mode… 1.23e8 Matias
6 Chacarita <NA> ((-58.45261 -34.59584, -… 702905 Stud… 3.61e6 Bond
# ℹ 7 more variables: neighbourhood_group <lgl>, neighbourhood <chr>,
# room_type <chr>, price <int>, minimum_nights <int>,
# number_of_reviews <int>, last_review <chr>One-to-one
The first approach we review here is the one-to-one approach, where we place a dot on the screen for every point to visualise. We are going to use ggplot and plot the points by neighbourhood.
ggplot() +
geom_sf(data = listings, aes(color = neighbourhood))
We can visualise a bit better with a basemap
ggplot() +
base_map(st_bbox(listings), basemap = 'google-terrain', increase_zoom = 2) +
geom_sf(data = listings, aes(color = neighbourhood), size = 0.5, alpha = 0.5) +
theme(legend.position = "none")please cite: map data © 2020 Google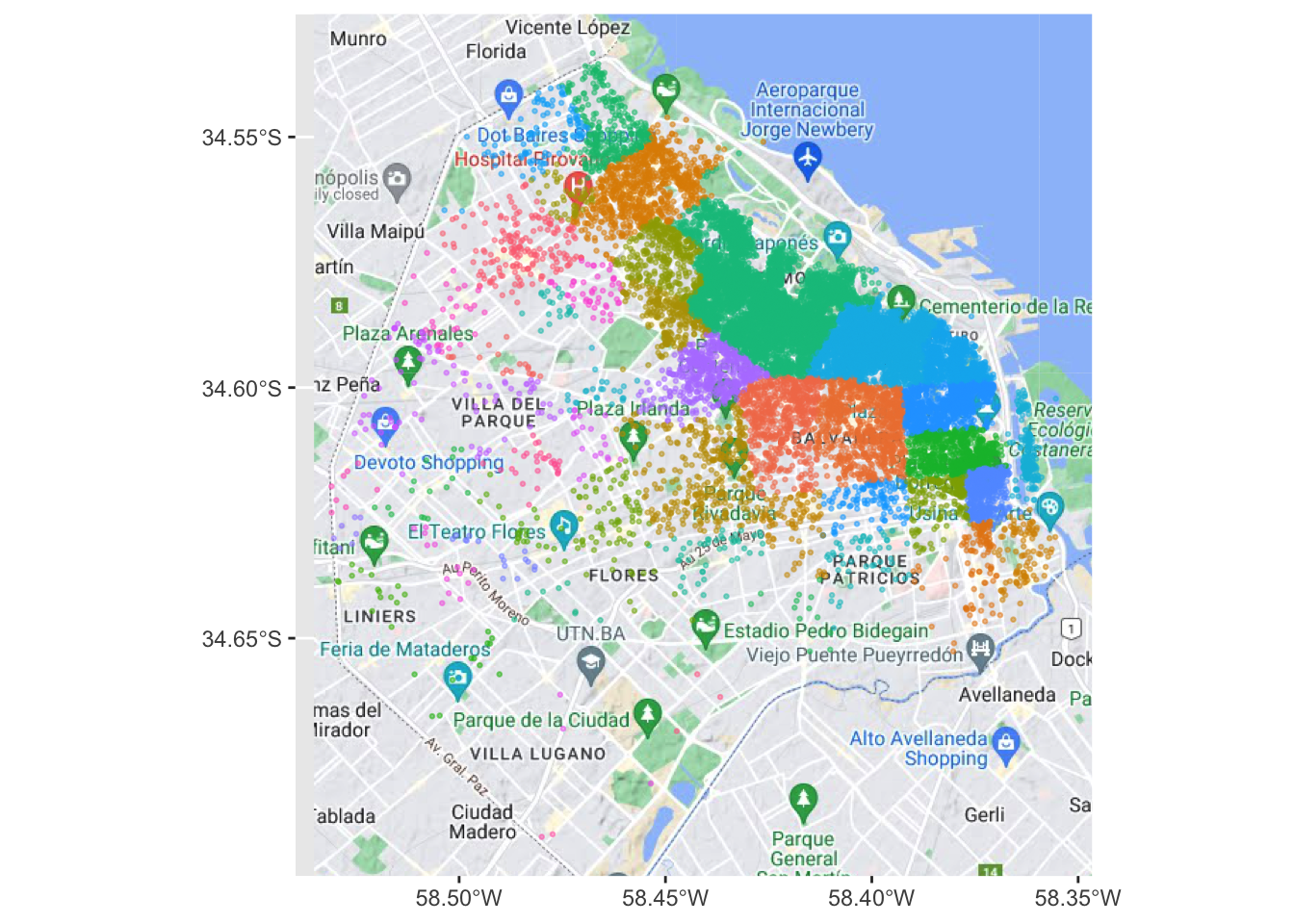
Points meet polygons
The approach presented above works until a certain number of points to plot; tweaking dot transparency and size only gets us so far and, at some point, we need to shift the focus. Having learned about visualizing lattice (polygon) data, an option is to “turn” points into polygons and apply techniques like choropleth mapping to visualize their spatial distribution. To do that, we will overlay a polygon layer on top of the point pattern, join the points to the polygons by assigning to each point the polygon where they fall into, and create a choropleth of the counts by polygon.
This approach is intuitive but of course raises the following question: what polygons do we use to aggregate the points? Ideally, we want a boundary delineation that matches as closely as possible the point generating process and partitions the space into areas with a similar internal intensity of points. However, that is usually not the case, no less because one of the main reasons we typically want to visualize the point pattern is to learn about such generating process, so we would typically not know a priori whether a set of polygons match it. If we cannot count on the ideal set of polygons to begin with, we can adopt two more realistic approaches: using a set of pre-existing irregular areas or create a artificial set of regular polygons. Let’s explore both.
Irregular lattices
To exemplify this approach, we will use the administrative areas we have loaded above. Let’s add them to the figure above to get better context (unfold the code if you are interested in seeing exactly how we do this):
ggplot() +
geom_sf(data = BA, fill = NA, size = 1.5) +
geom_sf(data = listings, aes(color = neighbourhood), size = 0.5, alpha = 0.5) +
theme(legend.position="none")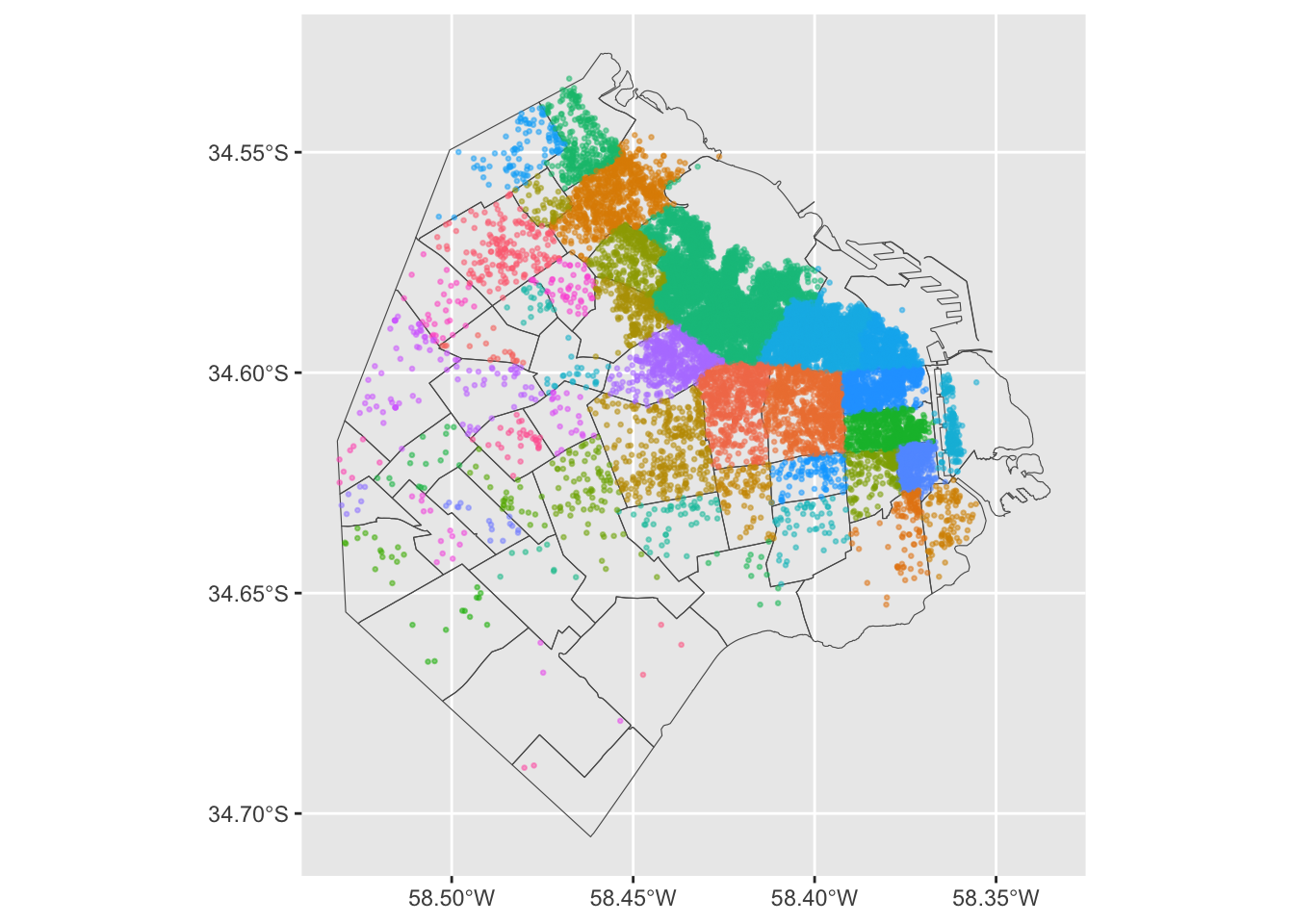
Now we need to know how many airbnb each area contains. Our airbnb table already contains the neighbourhood ID following our use of st_join. Now, all we need to do is counting by area and attaching the count to the areas table. We can also calculate the mean price of each area.
We rely here on the group_by function which takes all the airbnbs in the table and group them by neighbourhood. Once grouped, we apply function n(), which counts how many elements each group has and returns a column indexed on the neighbourhood level with all the counts as its values. We end by assigning the counts to a newly created column in the table.
This chunk may take a bit longer to run:
# aggregate at district level
airbnb_neigh_agg <- listings_BA %>%
group_by(neighbourh) %>% # group at neighbourhood level
summarise(count_airbnb = n(), # create count
mean_price = mean(price)) # average price
head(airbnb_neigh_agg)Simple feature collection with 6 features and 3 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -58.50354 ymin: -34.6625 xmax: -58.33515 ymax: -34.53153
Geodetic CRS: WGS 84
# A tibble: 6 × 4
neighbourh count_airbnb mean_price geometry
<chr> <int> <dbl> <POLYGON [°]>
1 Agronomia 18 2295. ((-58.4769 -34.59453, -58.47671 -34.594, -…
2 Almagro 682 3803. ((-58.41312 -34.61342, -58.41332 -34.61285…
3 Balvanera 930 2920. ((-58.41213 -34.5993, -58.41226 -34.60011,…
4 Barracas 123 11394. ((-58.37036 -34.63269, -58.37044 -34.63193…
5 Belgrano 807 4167. ((-58.45162 -34.53155, -58.45164 -34.53156…
6 Boca 99 2803. ((-58.3555 -34.61882, -58.35581 -34.61811,…The lines above have created a new column in our table called count_airbnb that contains the number of airbnb that have been taken within each of the polygons in the table. mean_price shows the mean price per neighbourhood.
At this point, we are ready to map the counts. Technically speaking, this is a choropleth just as we have seen many times before:
map_BA <- ggplot()+
geom_sf(data = airbnb_neigh_agg, inherit.aes = FALSE, aes(fill = count_airbnb), colour = "white") +
scale_fill_viridis("Count", direction = -1, option = "viridis" ) +
ggtitle("Count of Airbnbs by Neighbourhood") +
geom_sf_text(data = airbnb_neigh_agg,
aes(label = neighbourh),
fun.geometry = sf::st_centroid, size=2) +
theme_void()
map_BA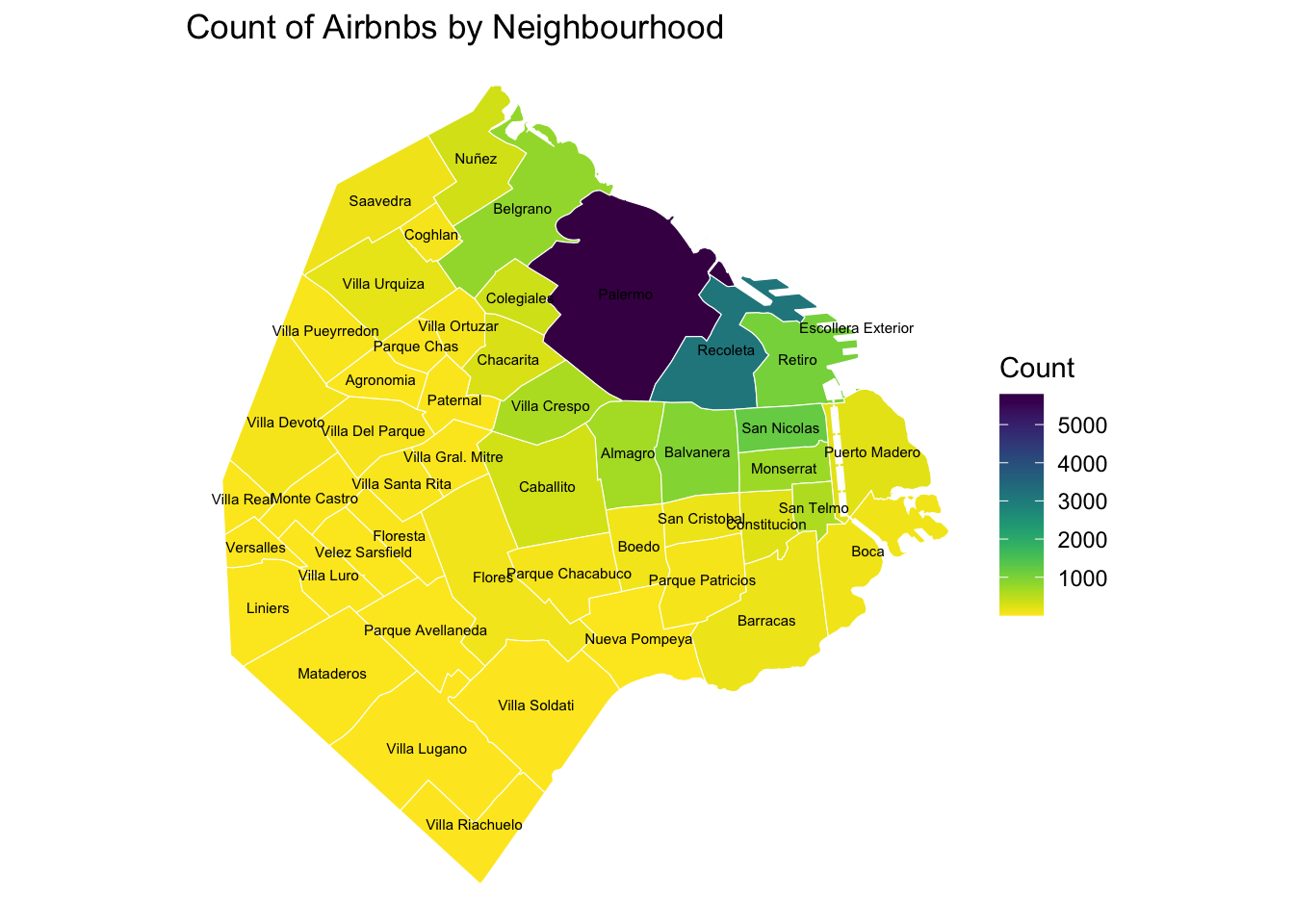
The map above clearly shows a concentration of airbnb in the neighbourhoods of Palermo and Recoleta. However, it is important to remember that the map is showing raw counts. In the case of airbnbs, as with many other phenomena, it is crucial to keep in mind the “container geography” (MAUP). In this case, different administrative areas have different sizes. Everything else equal, a larger polygon may contain more photos, simply because it covers a larger space. To obtain a more accurate picture of the intensity of photos by area, what we would like to see is a map of the density of photos, not of raw counts. To do this, we can divide the count per polygon by the area of the polygon.
Let’s first calculate the area in Sq. metres of each administrative delineation:
# Calculate area in square kilometers and add it to the data frame
airbnb_neigh_agg <- airbnb_neigh_agg %>%
mutate(area_km2 = as.numeric(st_area(.) / 1e6)) # 1e6 just means 1000000
# Calculate density
airbnb_neigh_agg <- airbnb_neigh_agg %>%
mutate(density = count_airbnb / area_km2)With the density at hand, creating the new choropleth is similar as above (check the code in the expandable):
map_BA_density <- ggplot()+
geom_sf(data = airbnb_neigh_agg, inherit.aes = FALSE, aes(fill = density), colour = "white") +
scale_fill_viridis("Density", direction = -1, option = "viridis") +
ggtitle("Density of Airbnbs by Neighbourhood") +
geom_sf_text(data = airbnb_neigh_agg,
aes(label = neighbourh),
fun.geometry = sf::st_centroid, size=2) +
theme_void()
map_BA_density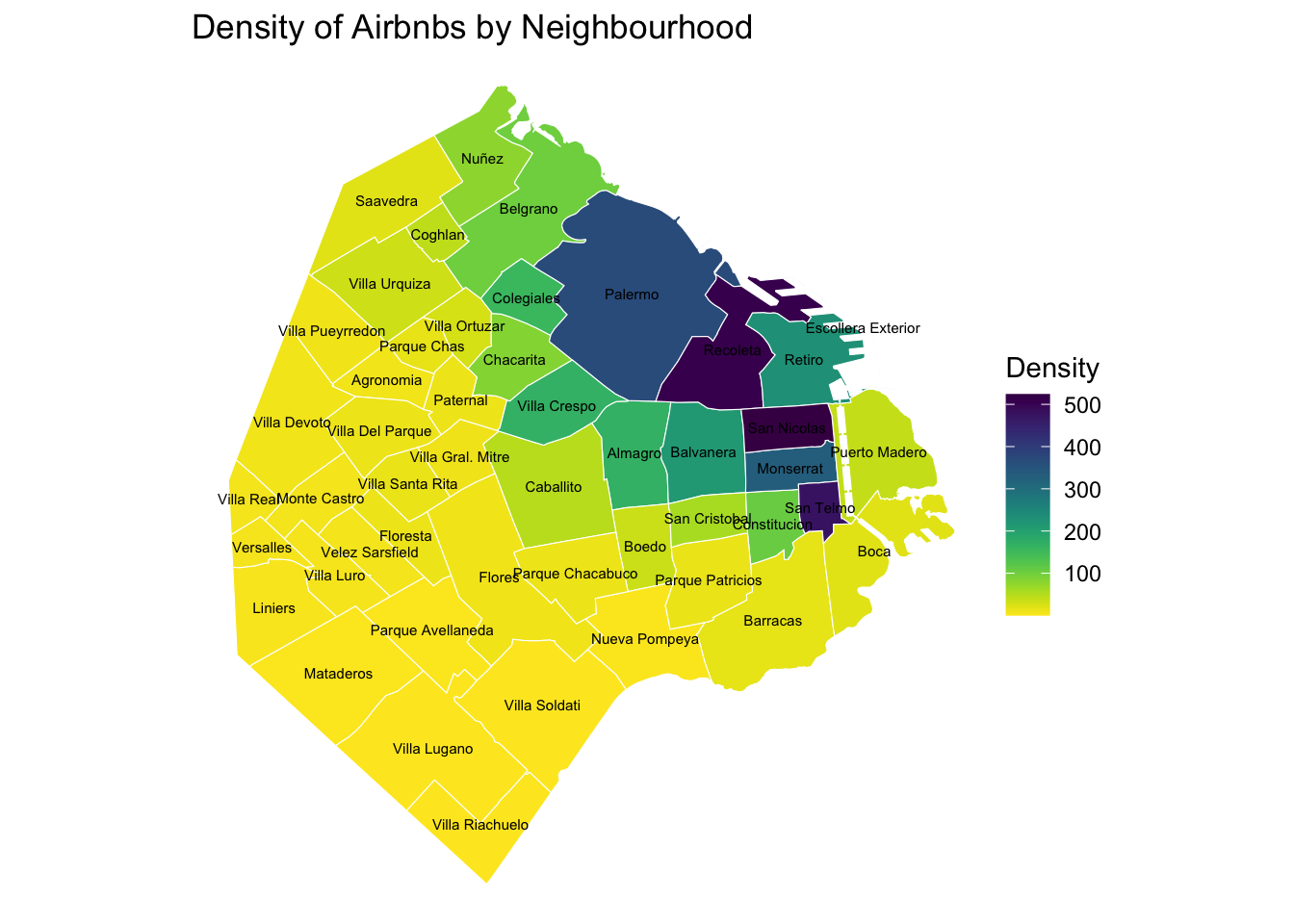
We can see some significant differences. Why is that? Have a chat with the person next to you.
Regular lattices: hex-binning
Sometimes we either do not have any polygon layer to use or the ones we have are not particularly well suited to aggregate points into them. In these cases, a sensible alternative is to create an artificial topology of polygons that we can use to aggregate points. There are several ways to do this but the most common one is to create a grid of hexagons. This provides a regular topology (every polygon is of the same size and shape) that, unlike circles, cleanly exhausts all the space without overlaps and has more edges than squares, which alleviates edge problems.
First we need to make sure we are in a projected coordinated system:
BA_proj <- st_transform(BA, 22176) # CRS for Argentina
listings_proj <- st_transform(listings, st_crs(BA_proj)) # Making sure both files have the same crs
# You can plot to check the data overlaps correctly
# plot(BA$geometry)
# plot(listings$geometry, add=TRUE)Then we create a grid that’s 500 metre by 500 metres. We need to be in a projected coordinate system for this to work.
grid <- st_make_grid(
BA_proj,
cellsize = 500,
crs = 4326,
what = "polygons",
square = FALSE) # creation of grid
plot(grid) # plot grid
To avoid any issues, convert the grid to an sf objects, which extends data.frame-like objects with a simple feature list column.
# Convert 'grid' to a simple features object
grid <- st_sf(grid)
# Add a new column 'n_airbnb' with counts of intersections with 'listings_proj'
grid <- grid %>% mutate(n_airbnb = lengths(st_intersects(grid, listings_proj)))
# Filter rows where 'n_airbnb' is greater than 1
grid_filtered <- filter(grid, n_airbnb > 1)Let’s unpack the coded here:
mutate: This is a function from thedplyrpackage we’ve used many times before and it is used to add new variables or modify existing variables in a data frame.lengths: This function is used to compute the lengths of the elements in a list. Here, it is applied to the result of thest_intersectsfunction.st_intersects(grid, listings_proj): This is a spatial operation using thesfpackage. It checks for spatial intersections between the objects in the grid and listings_proj data frames. This operation returns a list where each element corresponds to the intersections of a grid cell with the listings.- The result of
st_intersectsis passed tolengthsto determine the number of intersections for each grid cell.
The final result is that a new variable n_airbnb is added to the grid data frame, representing the number of intersections (or occurrences) for each grid cell with the listings in listings_proj.
# map manual
tmap_mode("view")
tm_shape(grid_filtered) +
tm_fill("n_airbnb",style="fixed", title = "Airbnb counts", alpha = .60, breaks=c(1, 10, 25, 50, 200, 500, 1000, Inf), palette = "-viridis")Kernel Density Estimation
Using a hexagonal binning can be a quick solution when we do not have a good polygon layer to overlay the points directly and some of its properties, such as the equal size of each polygon, can help alleviate some of the problems with a “bad” irregular topology (one that does not fit the underlying point generating process). However, it does not get around the issue of the modifiable areal unit problem (M.A.U.P.: at the end of the day, we are still imposing arbitrary boundary lines and aggregating based on them, so the possibility of mismatch with the underlying distribution of the point pattern is very real.
One way to work around this problem is to avoid aggregating into another geography altogether. Instead, we can aim at estimating the continuous observed probability distribution. The most commonly used method to do this is the so called kernel density estimate (KDE). The idea behind KDEs is to count the number of points in a continious way. Instead of using discrete counting, where you include a point in the count if it is inside a certain boundary and ignore it otherwise, KDEs use functions (kernels) that include points but give different weights to each one depending of how far of the location where we are counting the point is.
The actual algorithm to estimate a kernel density is not trivial but its application in R is rather simplified by the use of thespatstat or eks package.
Spatstat package
We first need to get the data into spatstat format from the spatstat package.
- This package is designed to work with points stored as
pppobjects and not SpatialPointsDataFrame orsfobjects - Note that a
pppobject may or may not have attribute information (also referred to as marks). - We will only concern ourselves with the pattern generated by the points and not their attributes
Point patterns in spatstat are objects of class ppp that contain points and an observation window (an object of class owin). We can create a ppp from points by where we see that the bounding box of the points is used as observation window when no window is specified.
# Transform the Buenos Aires neighbourhood file to
BA_owin <- as.owin(BA_proj)
BA_owin <- rescale(BA_owin, 1000)
# Transform listing to ppp object
listings_ppp <- as.ppp(listings_proj) # We can create a `ppp` object, object needs to be projectedWarning in as.ppp.sf(listings_proj): only first attribute column is used for
marksmarks(listings_ppp) <- NULL #remove all marks from point object
listings_ppp <- rescale(listings_ppp, 1000)
Window(listings_ppp) <- BA_owin # Creating window. Many point pattern analyses such as the average nearest neighbor analysis should have their study boundaries explicitly defined. This can be done in spatstat by “binding” the extent polygon to the point feature object using the Window() function.We then plot ppp just to check all is well.
plot(listings_ppp, main=NULL, cols=rgb(0,0,0,.2), pch=20)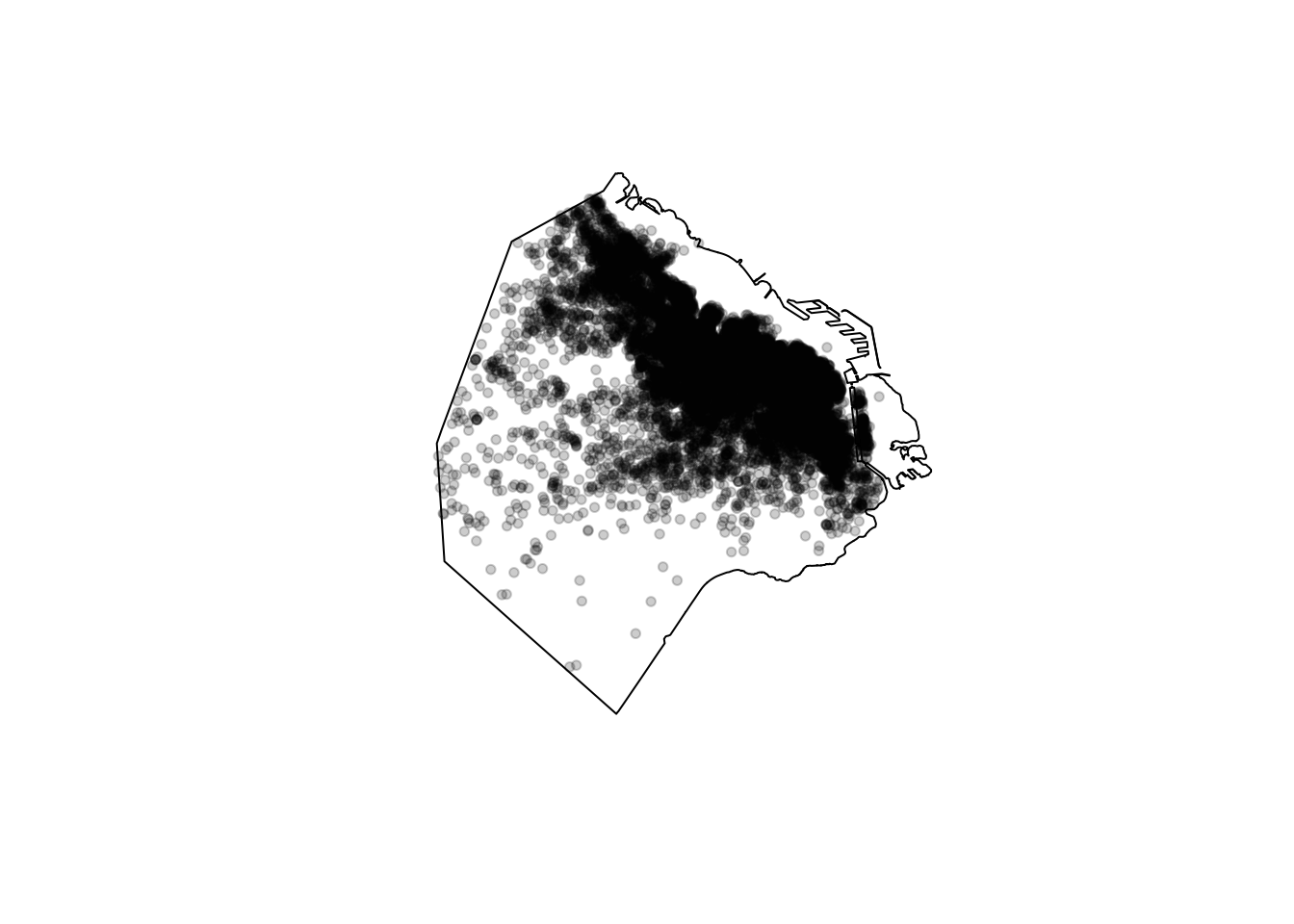
Kernel densities
Kernel densities can be computed using the function density, where kernel shape and bandwidth can be controlled. Below we specify the sigma and type of kernel.
sigma: The smoothing bandwidth (the amount of smoothing). The standard deviation of the isotropic smoothing kernel. Either a numerical value, or a function that computes an appropriate value of sigma.kernel: The smoothing kernel. A character string specifying the smoothing kernel (current options are “gaussian”, “epanechnikov”, “quartic” or “disc”), or a pixel image (object of class “im”) containing values of the kernel, or a function(x,y) which yields values of the kernel.
For more have a look here.
plot(density(listings_ppp, sigma=0.4, kernel="epanechnikov"))
plot(BA_owin, add = TRUE)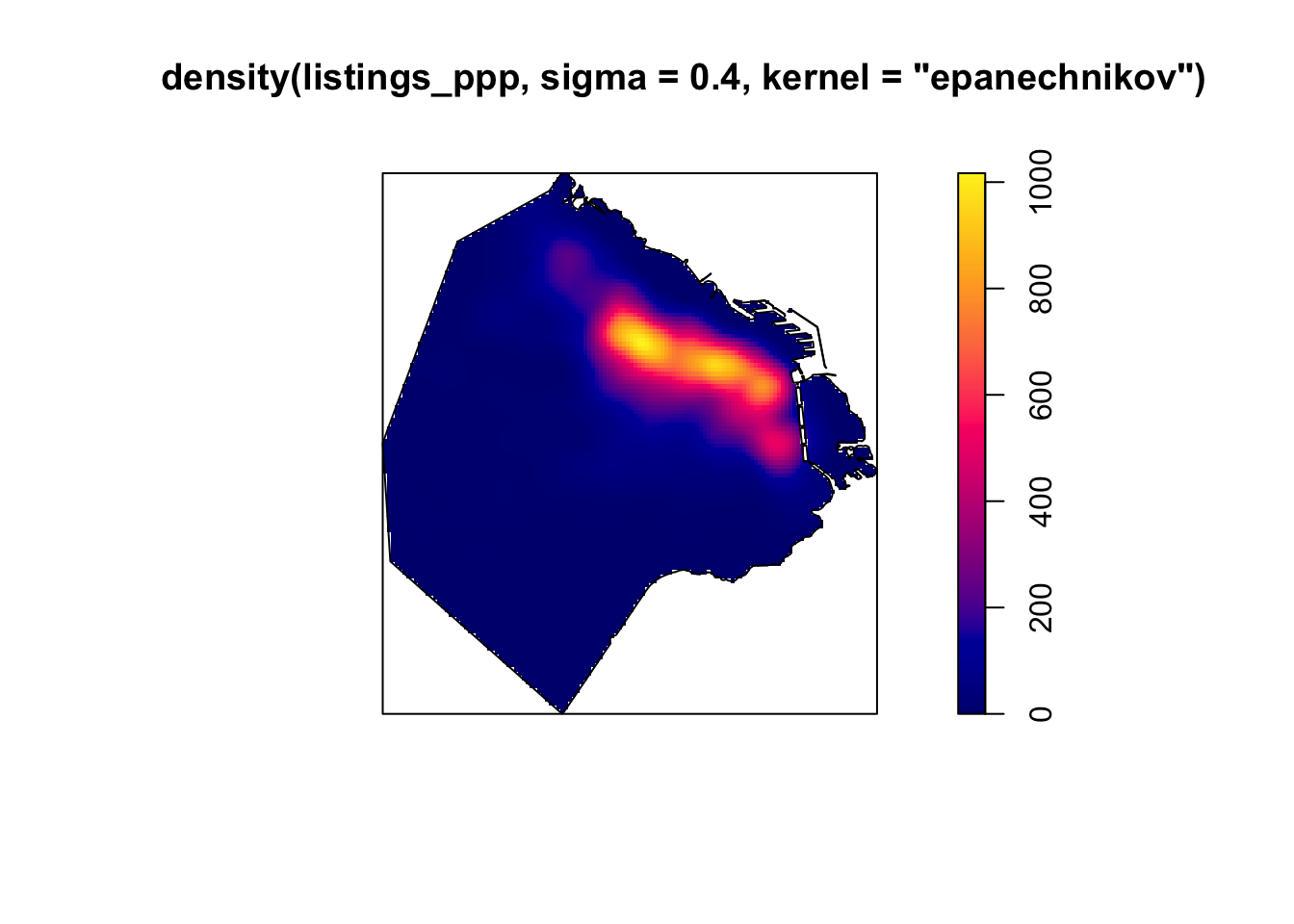
Here, cross validation is used by function bw.diggle to specify the bandwidth parameter sigma. To perform automatic bandwidth selection using cross-validation, it is recommended to use the functions bw.diggle, bw.CvL, bw.scott or bw.ppl.
plot(density(listings_ppp,sigma=bw.diggle(cells)))
plot(BA_owin, add = TRUE)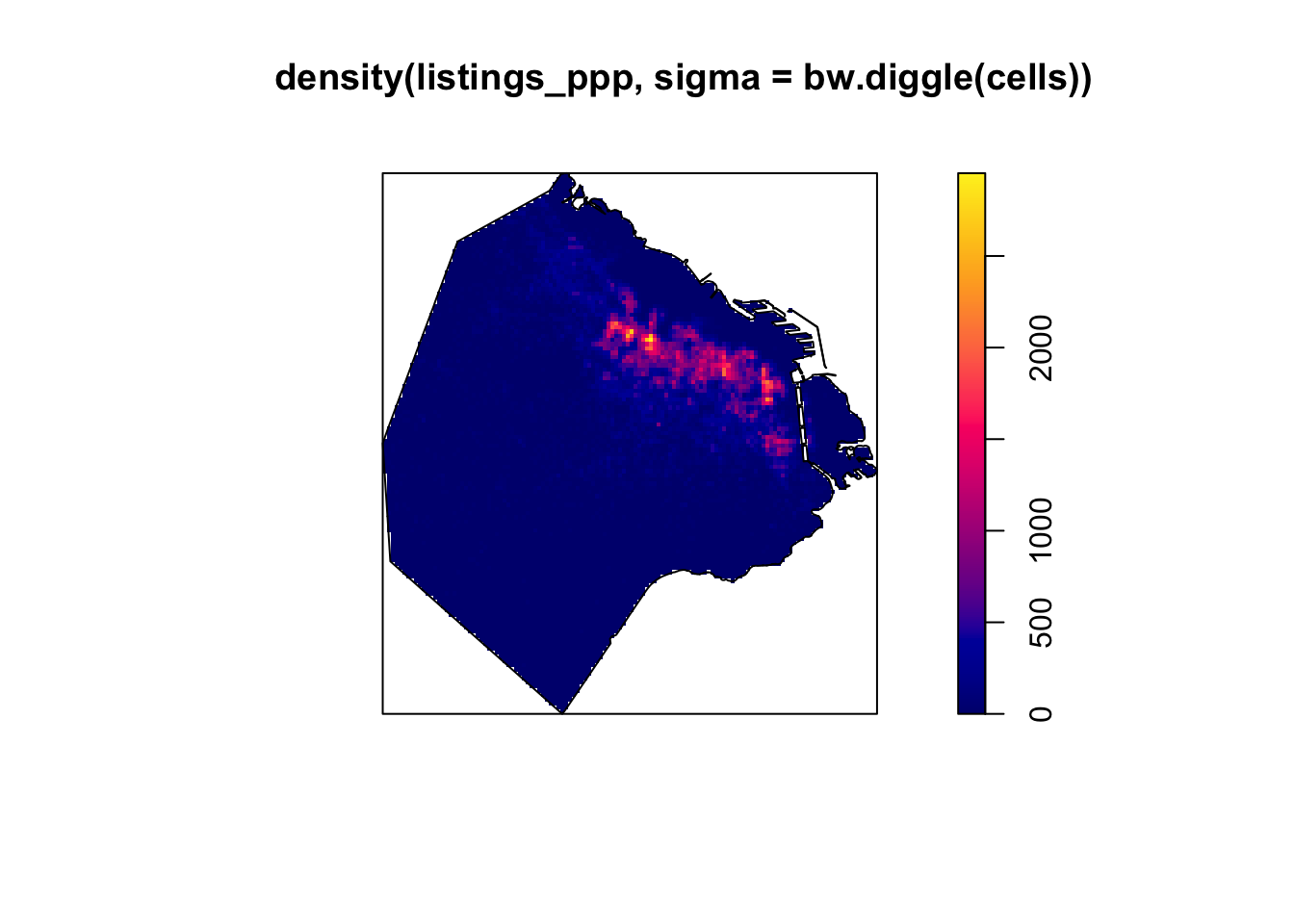
Or we can do Quadrat density
Or we can do Quadrat density
Q <- quadratcount(listings_ppp, nx= 6, ny=3)
plot(listings_ppp, pch=20, cols="grey70", main=NULL) # Plot points
plot(Q, add=TRUE) # Add quadrat grid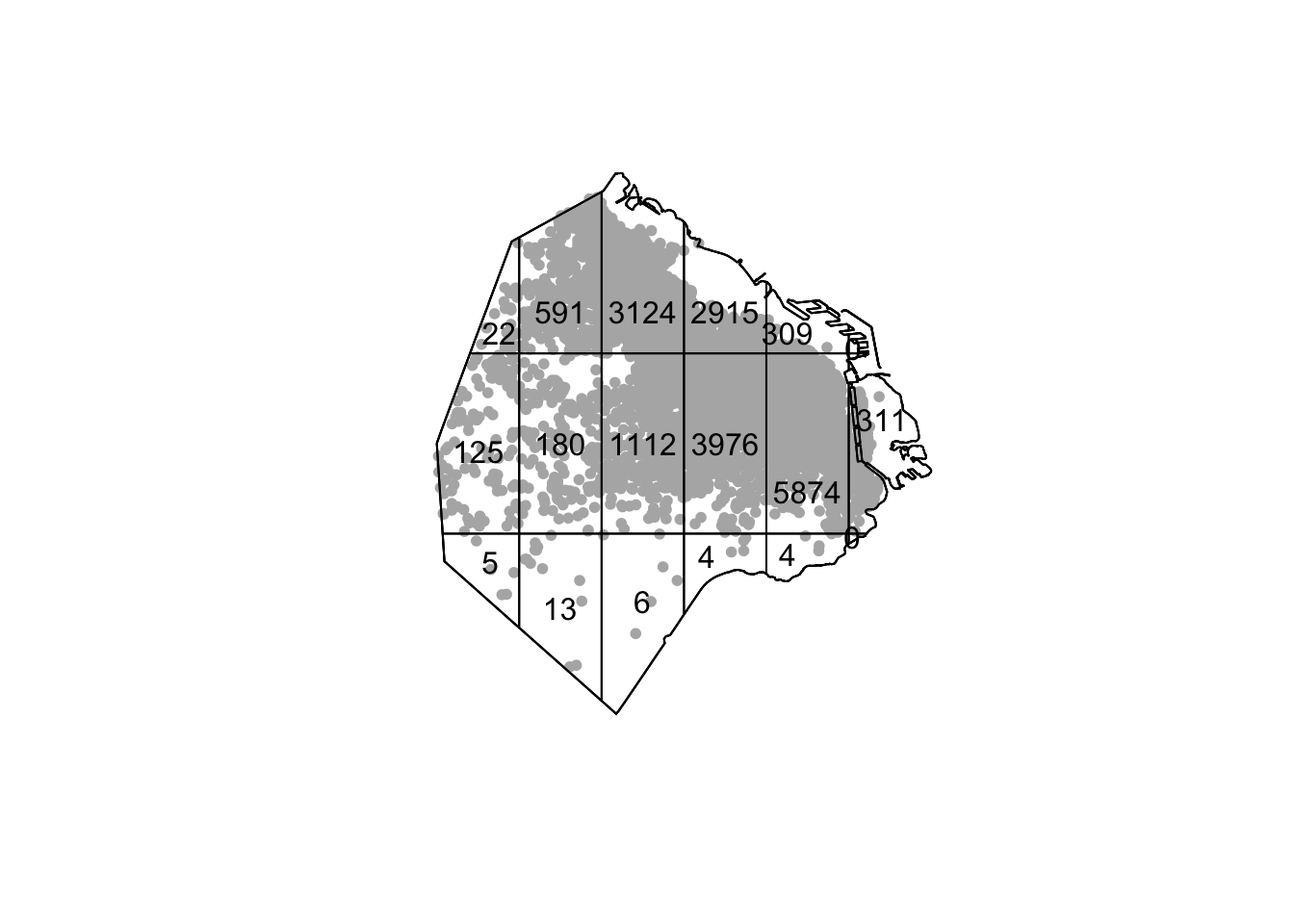
# Compute the density for each quadrat
Q.d <- intensity(Q)
# Plot the density
plot(intensity(Q, image=TRUE), main=NULL, las=1) # Plot density raster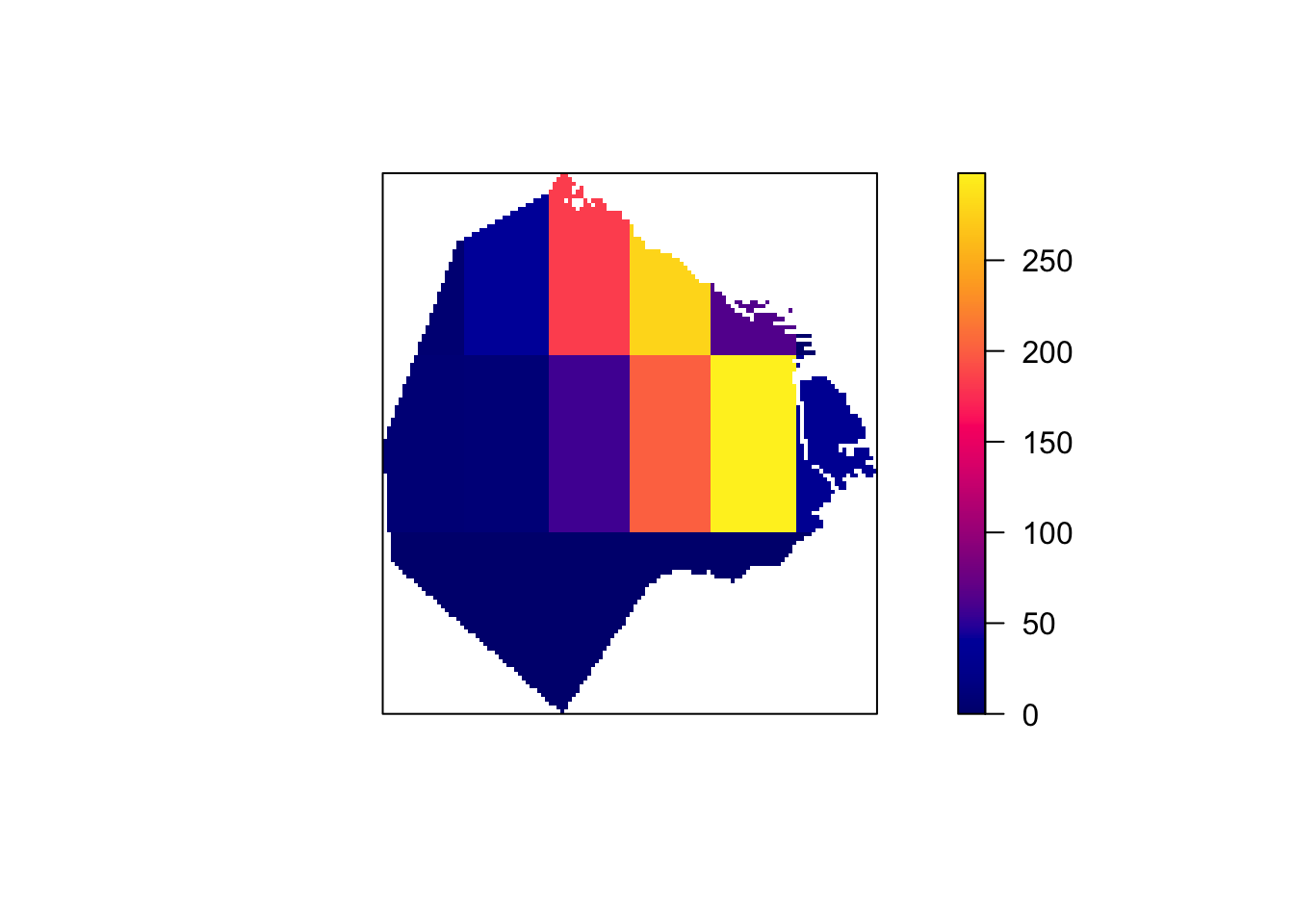
We can also use the density function and then convert density_spatstat into a stars object to then plot with ggplot. Check here for more details.
# use density function
density_spatstat <- density(listings_ppp)
# convert into a stars object
density_stars <- stars::st_as_stars(density_spatstat)
#Convert density_stars into an sf object
density_sf <- st_as_sf(density_stars) %>%
st_set_crs(22176)USe ggplot to visualise it.
ggplot() +
geom_sf(data = density_sf, aes(fill = v), col = NA) +
scale_fill_viridis_c() +
theme_void()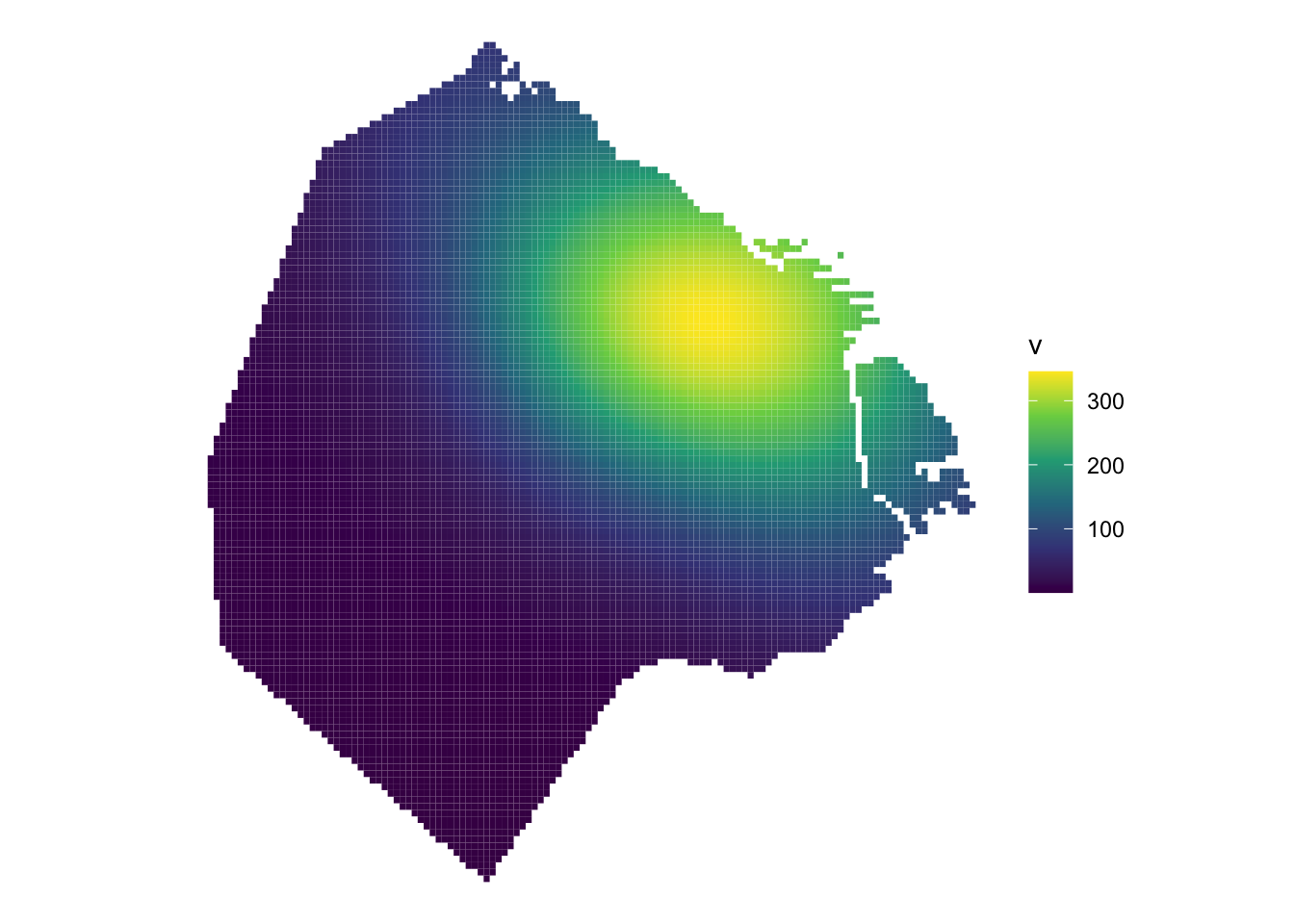
There is an alternative using the package eks which can be useful for final visualisations.
Kernel density can be computed with st_kde. The calculations of the KDE, including the bandwidth matrix fo smoothing parameters, are the same as in tidy_kde. For display, it is a matter of selecting the appropriate contour regions. The quartile contours 25%, 50%, 75% are selected by default in geom_contour_filled_ks for tidy data.
skde1 <- st_kde(listings_proj)
# Plot with ggplot
gs <- ggplot(skde1)
gs + geom_sf(data=listings_proj, col=8, size=0.5) +
geom_sf(data=st_get_contour(skde1), colour=1, fill=NA, show.legend=FALSE) +
theme_void()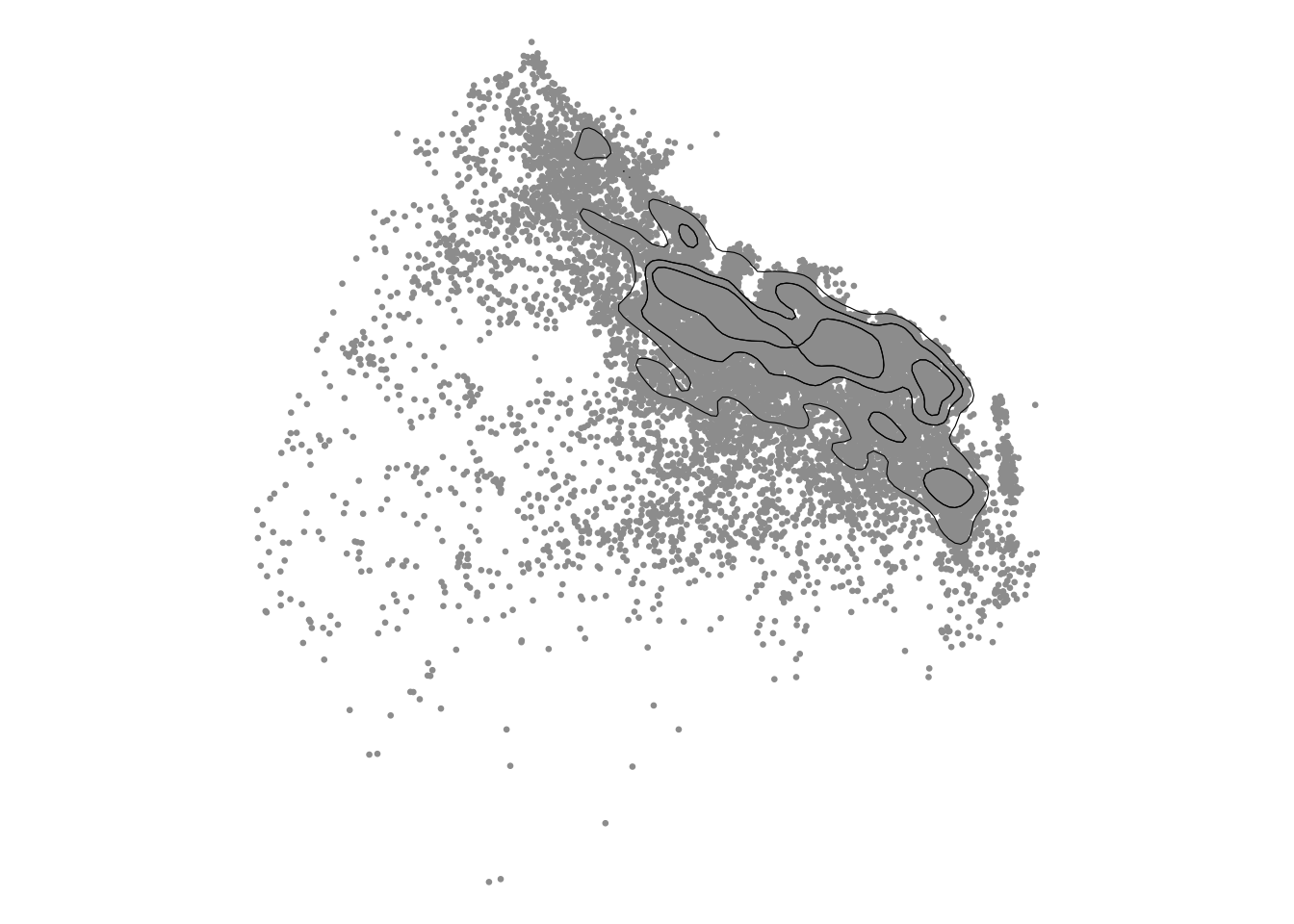
geom_sf filled contours
# geom_sf filled contour
gs + geom_sf(data=st_get_contour(skde1), aes(fill=label_percent(contlabel))) +
scale_fill_discrete_sequential(palette = "Blues") +
geom_sf(data=BA_proj, fill=NA) +
theme_void()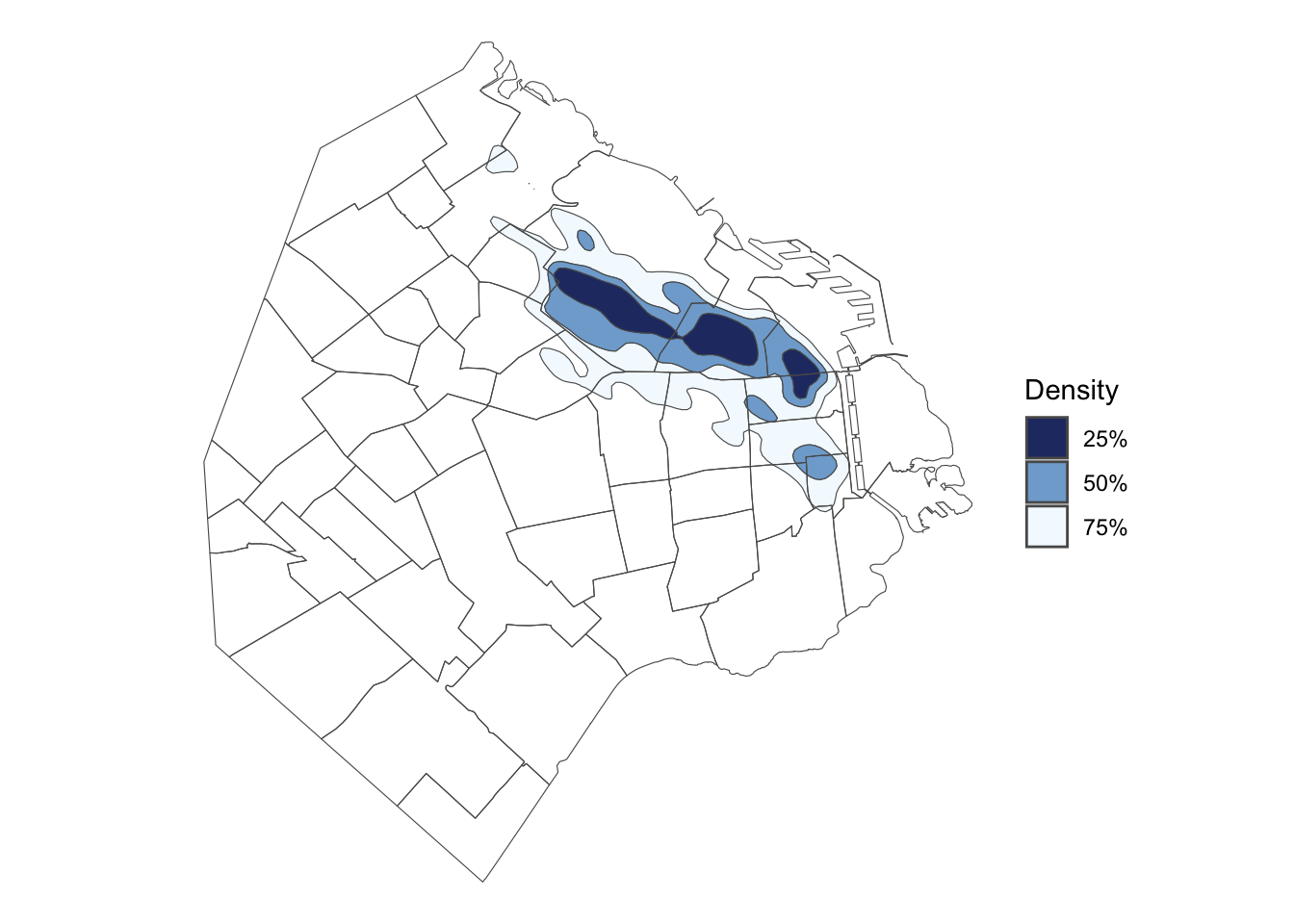
To generate a filled contour plot, the only required changes are to input an appropriate colour scale function with scale_fill_discrete_sequential. Have a look at help(scale_fill_binned_sequential).
Cluster of points (DBSCAN)
Partitioning methods (K-means, PAM clustering) and hierarchical clustering are suitable for finding spherical-shaped clusters or convex clusters. In other words, they work well for compact and well separated clusters. Moreover, they are also severely affected by the presence of noise and outliers in the data.
Unfortunately, real life data can contain: i) clusters of arbitrary shape ii) many outliers and noise.
In this section, we will learn a method to identify clusters of points, based on their density across space. To do this, we will use the widely used DBSCAN algorithm. For this method, a cluster is a concentration of at least m points, each of them within a distance of r of at least another point in the cluster. Points in the dataset are then divided into three categories:
- Noise, for those points outside a cluster.
- Cores, for those points inside a cluster whith at least
mpoints in the cluster within distancer. - Borders for points inside a cluster with less than
mother points in the cluster within distancer.
Both m and r need to be prespecified by the user before running DBSCAN. This is a critical point, as their value can influence significantly the final result. Before exploring this in greater depth, let us get a first run at computing DBSCAN.
In R we use the following packages to compute DBSCAN for real data.
dbscan: package which implements the DBSCAN algorithmfpc: flexible procedures for clustering
Data preparation for DBSCAN.
In preparing the data we are going to subset only the variables that we will need for the analysis. These include the location and the id of the stations.
listings <- read.csv("data/BuenosAires/listings_nooutliers.csv")
vars <- c("id","latitude","longitude")
d.sub <- dplyr::select(listings,vars)
head(d.sub) id latitude longitude
1 6283 -34.60523 -58.41042
2 11508 -34.58184 -58.42415
3 12463 -34.59777 -58.39664
4 13095 -34.59348 -58.42949
5 13096 -34.59348 -58.42949
6 13097 -34.59348 -58.42949Clustering by location.
locs = dplyr::select(d.sub,latitude,longitude)
# scalling the data points.
locs.scaled = scale(locs,center = T,scale = T)
head(locs.scaled) latitude longitude
[1,] -0.7138005 0.1575170
[2,] 0.5923367 -0.3100383
[3,] -0.2973356 0.6267068
[4,] -0.0576323 -0.4918842
[5,] -0.0576323 -0.4918842
[6,] -0.0576323 -0.4918842Computing DBSCAN using dbscan package
Load in all functions from the dbscan package
First, we set the ‘random seed’, which means that the results will always be the same when running the following commands, since the random aspects of the algorithms are controlled.
set.seed(123456789)Run the DBSCAN algorithm, specifying:
eps: ‘epsilon’, radius of the ‘epsilon neighborhood’ (the maximum point-to-point distance for considering two points to be in the same cluster)minPts: the minimum number of points required to be in the ‘epsilon neighborhoods’ of core points (including the point itself).- Note that ‘core points’ refer to points which are within the ‘epsilon neighborhood’ of the randomly selected starting point.
db <- dbscan::dbscan(locs.scaled, eps=0.10, minPts = 10)
dbDBSCAN clustering for 18572 objects.
Parameters: eps = 0.1, minPts = 10
Using euclidean distances and borderpoints = TRUE
The clustering contains 19 cluster(s) and 860 noise points.
0 1 2 3 4 5 6 7 8 9 10 11 12
860 17199 70 116 38 37 20 64 10 13 16 21 23
13 14 15 16 17 18 19
10 11 16 14 10 14 10
Available fields: cluster, eps, minPts, dist, borderPointsUse the results from applying dbscan to plot the example data once more, coloring points according to which cluster dbscan grouped each point in. In the dbscan results, cluster group ‘0’, plotted below in black, indicates ‘noise points’. A ‘noise point’ is one which isn’t close enough to (‘minPts’ - 1) number of other points to be considered part of any cluster.
factoextra::fviz_cluster(db,locs.scaled,stand = F,ellipse = T,geom = "point") + theme_minimal() 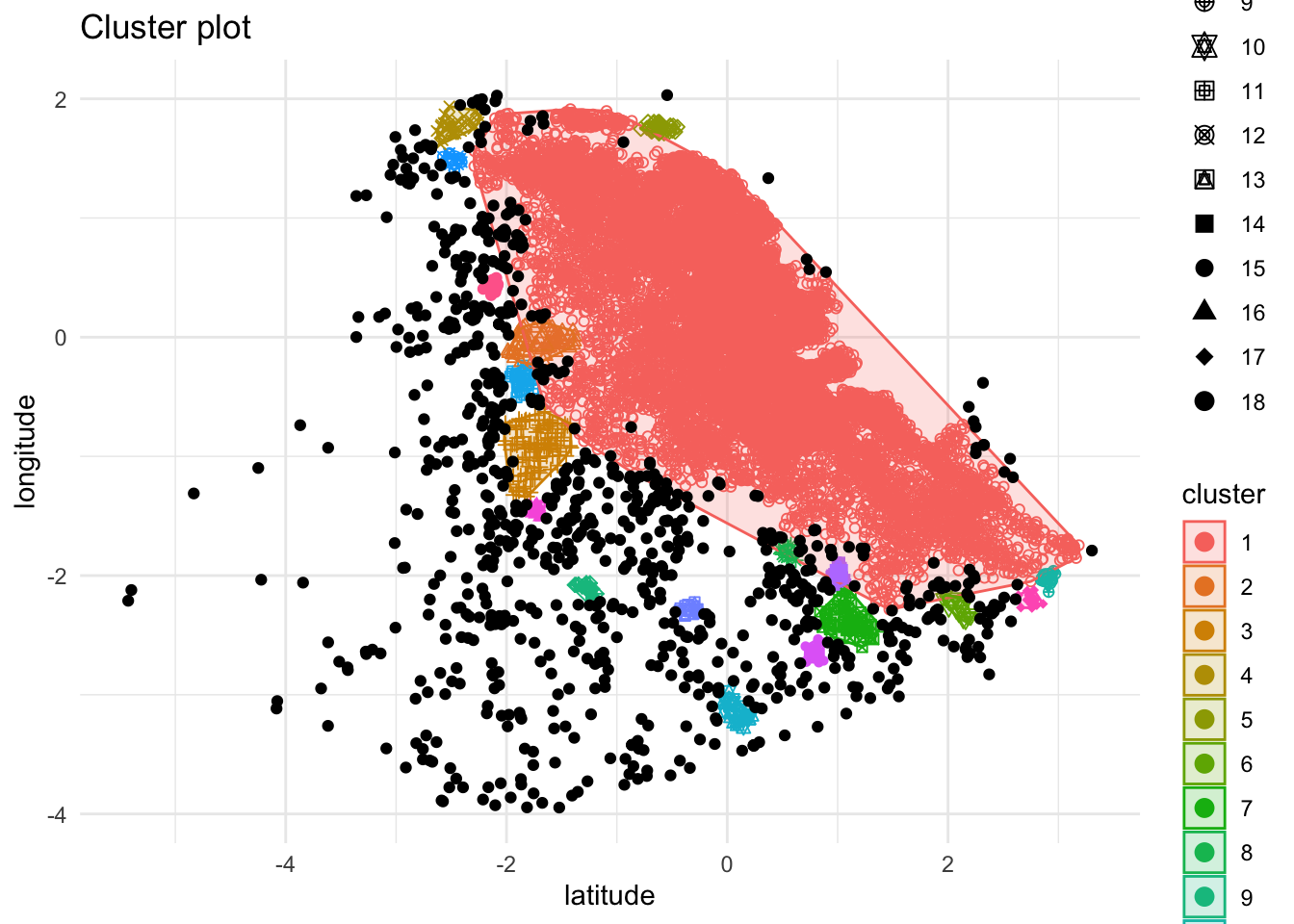
This needs some cleaning up, but you get the idea.
You can also display the results of the dbscan.
print(db)DBSCAN clustering for 18572 objects.
Parameters: eps = 0.1, minPts = 10
Using euclidean distances and borderpoints = TRUE
The clustering contains 19 cluster(s) and 860 noise points.
0 1 2 3 4 5 6 7 8 9 10 11 12
860 17199 70 116 38 37 20 64 10 13 16 21 23
13 14 15 16 17 18 19
10 11 16 14 10 14 10
Available fields: cluster, eps, minPts, dist, borderPointsThe dbscan algorithm is very sensitive to changes to the epsilon and minPts values. Smaller epsilons leads to definition of sparser clusters as noise while larger epsilon sizes may make denser clusters to be merged.
Determining the optimal eps value.
To determine the optimal distance, think of every point and its average distance from its nearest neighbours. We can now use k-nearest neighbour distances matrix to compute this with a specified value of k corresponding to minPts.
We then plot these points in ascending order with an aim of aim of determining the “knee” which corresponds to the optimal eps parameter. The “knee” in this case is equivalent to a threshhold where a sharp change occurs along the k distance curve.
We can use the kNNdistplot() function from the dbscan package.
dbscan::kNNdistplot(locs.scaled,k=12)
abline(h=0.15,lty = 2,col=rainbow(1),main="eps optimal value")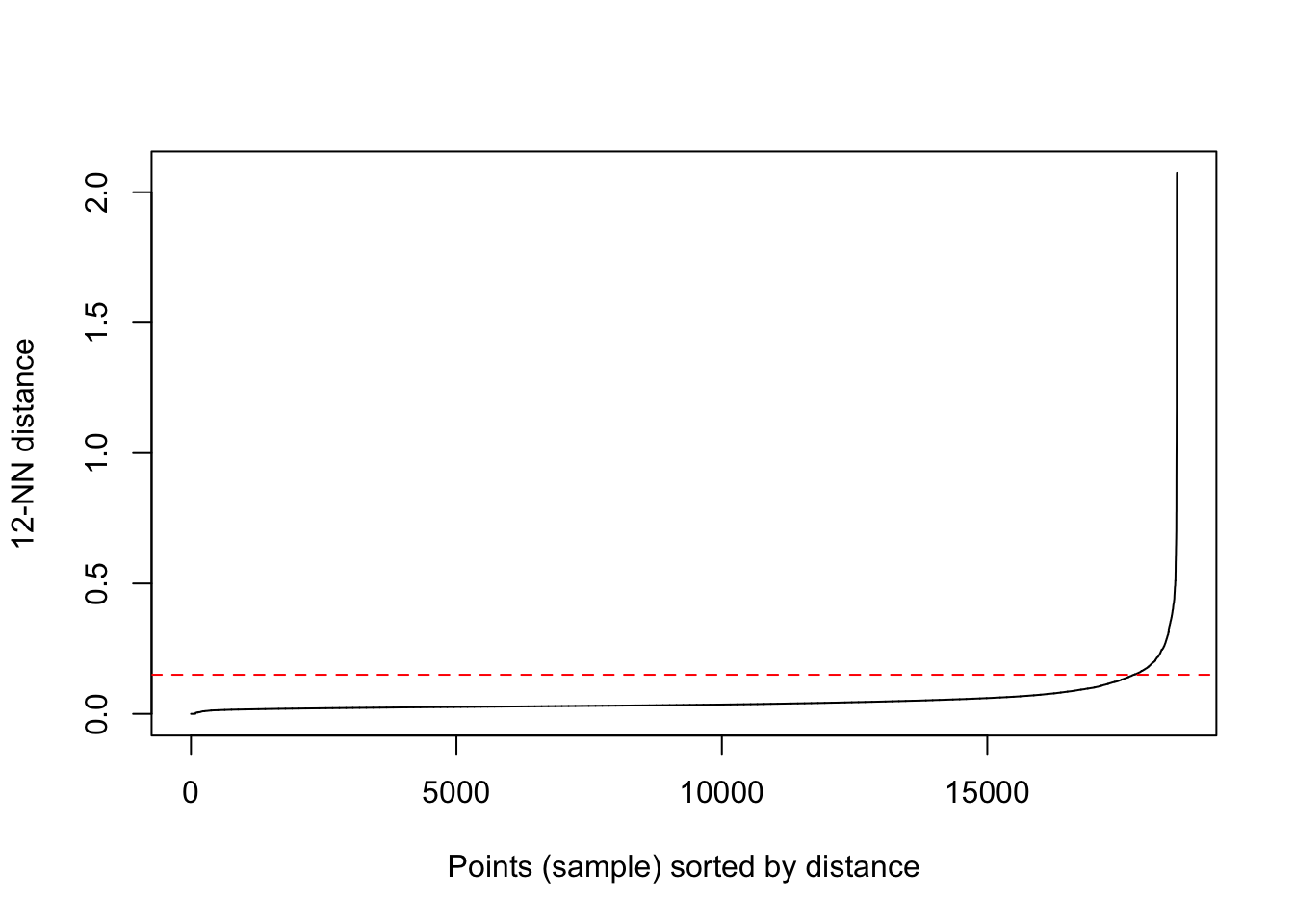
The optimal value of eps is around 0.10 from the chart above.
Interpolation
Please keep in mind this final section of the tutorial is OPTIONAL, so do not feel forced to complete it. This will not be covered in the assignment and you will still be able to get a good mark without completing it (also, including any of the following in the assignment does NOT guarantee a better mark).
Inverse Distance Weighting (IDW) is an interpolation technique where we assume that an outcome varies smoothly across space: the closer points are, the more likely they are to have the same outcome. To predict values across space, IDW uses neighbours values. There are two main variables: the number of neighbours to consider and the speed of the spatial decay. For example, if we were to model the likelihood of a household to shop at the neighbouring local groceries store, we would need to set a decay such as the probability would be close to 0 as we reach 15 minutes walking distance from home.
The typical problem is a missing value problem: we observe a property of a phenomenon \(Z(s)\) at a limited number of sample locations, and are interested in the property value at all locations covering an area of interest, so we have to predict it for unobserved locations. This is also called kriging, or Gaussian Process prediction.
Ordinary Kriging
We can Cceate geostatistical prediction using a ordinary Kriging and the package gstat.
gs <- gstat(formula = price~1, # formula that defines the dependent variable as a linear model of independent variables
data = listings_proj, # housesales data
nmax = 500, # the number of nearest observations that should be used
set=list(idp = 0.2)) # set inverse distance power Create a blank raster using district extent and crs
r <- raster(BA_proj, resolution=200) # output cell size Create the interpolated raster using the prediction from the model and the blank raster
# Interpolated raster using the prediction from the model
idw <- interpolate(r, gs)[inverse distance weighted interpolation]# Mask values outside Buenos Aires
idwr <- mask(idw, BA_proj)Plot the results
plot(idwr, col = rev(heat.colors(100)))
plot(BA_proj$geometry, fill = NA, add=T)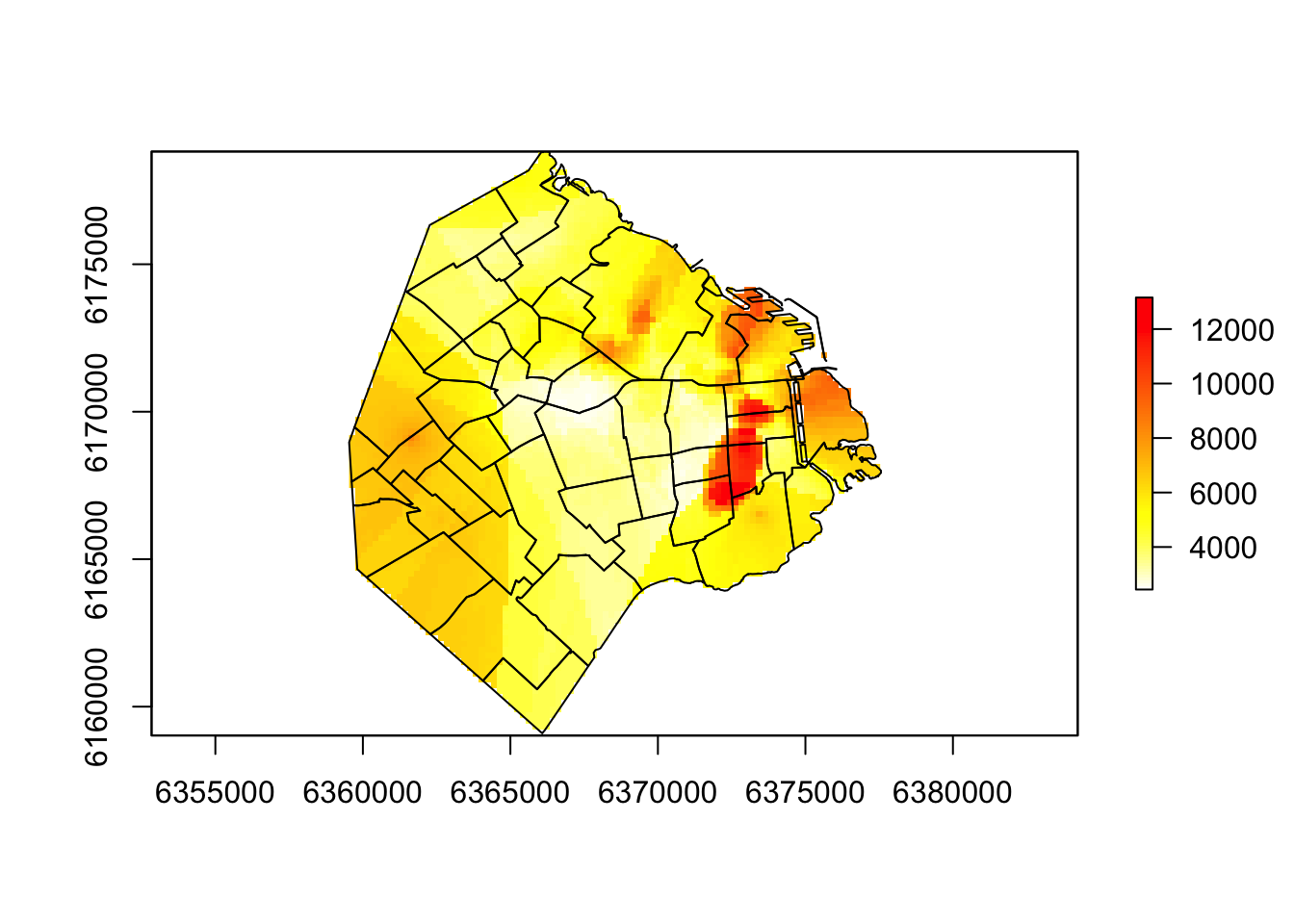
This would need a lot more work.
In the gstat formula, you can then play around with:
- Number of nearest observations
- Inverse distance power
- Output cell size 250
and decide how to best interpolate your data.